本文所用的计算程序是在美国Sandia国家实验室的5.M.Foiles等人的Mc92程序基础上结合Zhang和Hu等人改进的分析型EAM多体势改编而成。整个程序的大致框图如图3.4所示,现结合此图对整个计算程序作简单说明如下:
1.输入参数。输入参数包括原子层数,每层原子个数,两种合金元素的基本物理量(包括晶格类型,晶胞参数,弹性常数等),合金的晶格类型和表面方向及其旋转矩阵等等,所有这些参数全部放在一个输入文件mc92.i中,改变合金系统时不需要对计算程序作任何其他的修改。这样做的好处是简单方便,不易出错。
2.计算原子间的相互作用势。应用分析型EAM多体势模型计算元素的势函数,通过构筑的合金势即可计算合金体系在一定条件的总能量。原来Foiles使用的EAM模型为数值拟合的方法,无分析型形式,不能系统地推广应用。在我们修改的程序中已经应用Zhang和Hu等人发展的分析型EAM多体势函数,采用类似于Johnson的合金势形式,通过元素的基本物理性质即可预测合金表面的性质。详细的有关此分析型的EAM模型的说明见上一章,它非常易于推广至其它合金系统的物理性能的计算,具有相当大的普适性。
3.合金晶格的建立,按照晶体原胞在三维空间的周期性堆垛而构成。在计算体成分时,应用三维周期性边界条件,计算表面时在平行于表面的方向应用周期性边界条件,而在沿表面的法线方向则没有周期性边界条件。
4.原子的排序。在计算体成分时以到中心原子的距离由近至远的顺序来排序,计算表面聚集时以到表面的距离大小来排序,即原子是以一层一层的方式来排序。
5.计算初始态的能量。每个原子的能量由三部分组成,即对势部分、嵌入能部分和修正项部分。
6.执行基本的MonteCarlo模拟过程:随机选取一个将要移动的原子,随机决定其种类,然后用EAM多体势函数计算原子移动前后系统总能量的变化,再按照Metr叩0115算法决定这一步是否被接受。反复地重复这一过程,总的MonteCarlo步数为nsteps=ilooplXiloopZ步,在循环过程当中每隔ilooPZ步输出一组数据,最后采用分层抽样方法以减少方差。
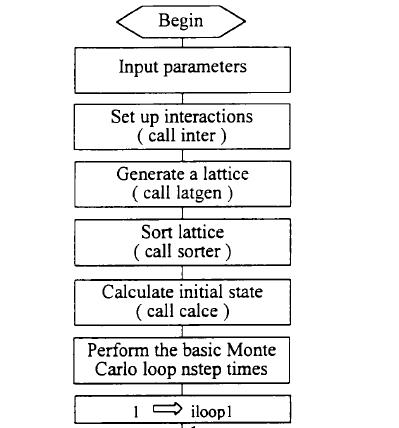 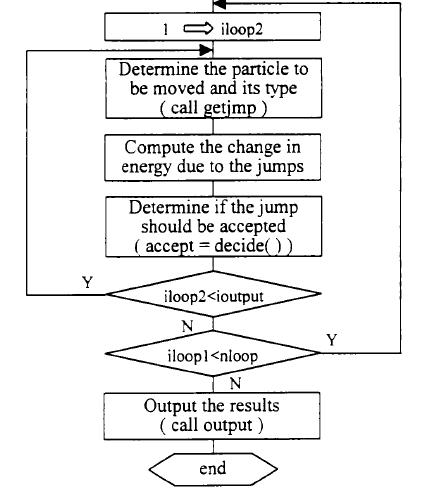
程序允许系统有三种不同的方式朝平衡态方向演化:(l)原子可以沿任意方向作小的位移—模拟原子的振动与弛豫:(2)原子的晶格常数可以变化—模拟晶格的热膨胀和收缩;(3)在总的原子数不变的情况下,原子类型可以任意变化东莞滴胶一一模拟合金中原子之间通过相互扩散而达到平衡状态。由此可见,本程序在模拟过程中自然而然地包含了振动嫡和组态墒的作用。
|